这里先给出题目
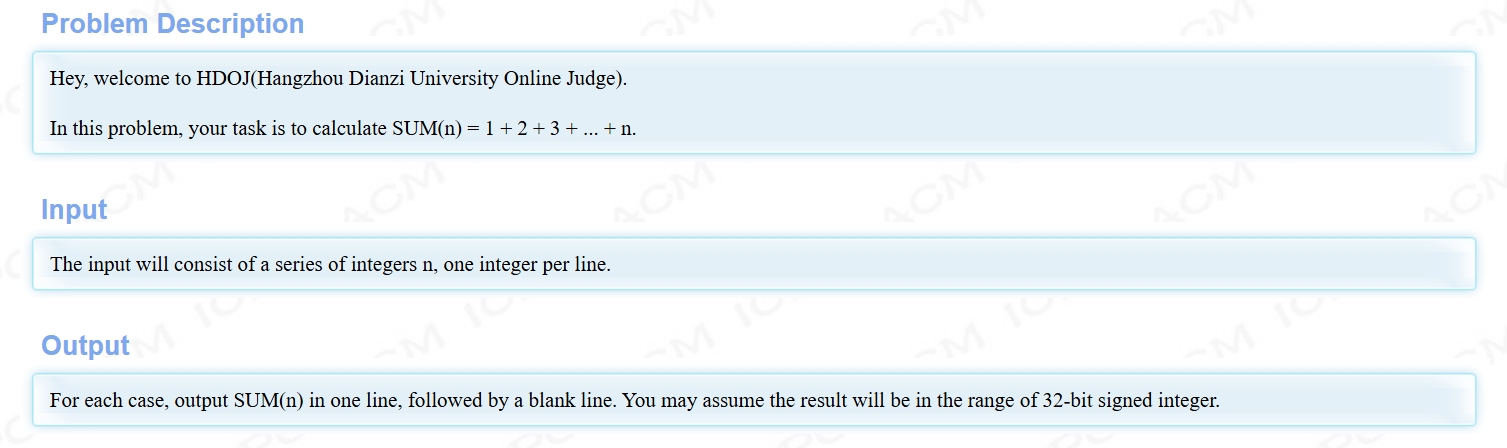
这道题让我们求从1到n的和,我们可以很自然的想到高中所学的等差数列求和公式S_n=\frac{n(a_1+a_n)}{2}
显然,我们只需让a_1=1,然后用函数传入一个n即可计算,如下函数代码(只展示函数的代码)
int sum(int n){
int ret;
ret = (n*(1+n))/2;
return ret;
}但当我们将代码提交的时候,会报Wrong answer,这是因为当传入的n特别大的时候,会超出int类型的范围,所以最保险还是用累加的方法
#include <iostream>
using namespace std;
int sum(int n){
int ret=0;
for(int i = 0;i<n;i++){
ret += i+1;
}
return ret;
}
int main() {
int n;
int ans;
while (cin >> n) {
ans = sum(n);
cout << ans << endl<< endl;
}
}到这里,问题已经解决,不过关于等差数列求和公式的解法,我们还可以进一步探索,事实上,原来的溢出问题是产生在n(n+1)的部分,但是我们可以先计算\frac{n}{2}(当n为偶数时)或者\frac{n+1}{2}(当n为奇数时),再将它们与另外一项相乘,这样就可以巧妙地化解溢出问题
int sum(int n){
if (n % 2 == 0) {
return (n + 1) * (n / 2);
}else{
return n * ((n + 1) / 2);
}
}