C语言课堂上的一些题目解答

近期在攻克C++指针的相关内容，HDOJ上做的题也比较简单，没有什么必要记录题解，故在这里写一下C语言课堂上的题目的题解（也不算很简单，这篇文章的代码均使用C语言实现）

1.简单四则运算计算器

键盘输入“第1操作数运算符第2操作数”，根据运算符（+、-、*、/）给出计算结果，例如：200/10=20

这道题就是接受三个输入（两个整数，还有一个计算符号），用三个变量接收后，根据计算符号匹配相应的操作符即可

#include <stdio.h>

int main() {
    int a, b;
    char sym;
    scanf("%d %c %d", &a, &sym, &b);
    if (sym == '+') {
        printf("%d\n", a + b);
    } else if (sym == '-') {
        printf("%d\n", a - b);
    } else if (sym == '*') {
        printf("%d\n", a * b);
    } else if (sym == '/') {
        if (b != 0) {
            printf("%d\n", a / b);
        } else {
            printf("Error: Division by zero\n");
        }
    } else {
        printf("Error: Unknown operator\n");
    }
}

也可以使用swich语句匹配操作符

#include <stdio.h>

int main() {
    int a, b;
    char sym;
    scanf("%d %c %d", &a, &sym, &b);
    switch (sym) {
        case '+':
            printf("%d\n", a + b);
            break;
        case '-':
            printf("%d\n", a - b);
            break;
        case '*':
            printf("%d\n", a * b);
            break;
        case '/':
            if (b != 0) {
                printf("%d\n", a / b);
            } else {
                printf("Error: Division by zero\n");
            }
            break;
        default:
            printf("Error: Unknown operator\n");
    }
}

总体来说还是一道很简单的一道题的

2.分段函数的计算

当x在区间[1，8]上时按下面的表达式计算函数否则y=0
f(x)=\begin{cases}3x+5&\ 1\leqslant x <2 \\2\sin x -1&\ 2\leqslant x<3 \\ \sqrt{1+x^2} &\ 3\leqslant x <5 \\ x^2-2x+5 &\ 5\leqslant x \leqslant 8 \end{cases}

这道题就是一个分段函数的题目，引入math头文件后就可以实现所有的运算，可以实现一个函数传入输入的x但是要注意传入的参数类型和返回值的类型都是double ，因为返回值为double 类型，在打印到控制台时可以格式化小数位数为两位数

#include <stdio.h>
#include <math.h>

double func(double x) {
    if (x < 1||x>8){
        return 0;
    }else if (x >= 1 && x < 2){
        return 3*x + 5;
    }else if (x >= 2 && x <3){
        return 2*sin(x)-1;
    }else if (x >= 3 && x < 5){
        return sqrt(1+x*x);
    }else if (x >= 5 && x <= 8){
        return x*x-2*x+5;
    }
}
int main(){
    double a;
    scanf("%lf", &a);
    double ans = func(a);
    printf("%.2lf\n", ans);
}

3.成绩转换

输入学生某科成绩（十进制整数），将百分制转换为字符表示的等级制：90--100分为‘A’级；80--89为‘B’级；70--79为‘C’级；60--69为‘D’级；其它为‘E’级

这个就是一道很经典的if语句练习题，没有什么好讲的

#include <stdio.h>

int main(){
    int score;
    char grade;
    scanf("%d", &score);
    if (score >= 90 && score <= 100){
        grade = 'A';
    }else if (score >= 80 && score < 90){
        grade = 'B';
    }else if (score >= 70 && score < 80){
        grade = 'C';
    }else if (score >= 60 && score < 70){
        grade = 'D';
    }else{
        grade = 'E';
    }
    printf("Grade: %c\n", grade);
    return 0;
}

4.最大三数

从键盘输入10个整数，输出其中最大的三个整数

这个题目我的第一想法是将十个整数放入一个数组中，然后对数组进行排序（我使用了冒泡排序），最后输出数组最后三个元素即可

冒泡排序：在待排序的一组数中，将相邻的两个数进行比较，若前面的数比后面的数大就交换两数，否则不交换；如此下去，直至最终完成排序。由此可得，在排序过程中，大的数据往下沉，小的数据往上浮，就像气泡一样，于是将这种排序算法形象地称为冒泡排序

#include <stdio.h>

int main(){
    int arr[10];
    for (int i = 0; i < 10; i++){
        scanf("%d", &arr[i]);
    }
    for (int i = 0; i < 10; i++){
        for (int j = 0; j < 9 - i; j++){
            if (arr[j] > arr[j + 1]){
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
    printf("%d %d %d",arr[7], arr[8], arr[9]);
}

不过这个方案有一个缺点，就是假如我们输入的不是10个整数，而是N个整数，那么我们就需要为数组分配很大的内存空间。我们可以再读一遍题目，发现我们只输出最大的三个数，所以我们只需要关心最大的三个数即可，那么我们可以引入三个变量来储存最大的三个数，对于输入的每一个数，我们判断它是否可以在已有的三个变量的大小区间内，从而不断更新最大的三个数。还有一个小问题，因为输入的数可能包含负数，所以我们不可以用0来作为三个数的初始化值，我们应该将它们初始化为-2147483648（int类型的最小值）

#include <stdio.h>

int main(){
    int n;
    int a=-2147483648, b=-2147483648, c=-2147483648;//int类型的最小值
    int tmp;
    scanf("%d", &n);
    for (int i = 0; i < n;i++){
        scanf("%d",&tmp);
        if (tmp > c){
            a = b;
            b = c;
            c = tmp;           
        } else if (tmp < c && tmp > b){
            a = b;
            b = tmp;
        } else if (tmp < b && tmp > a){
            a = tmp;
        }
    }
    printf("%d %d %d", a, b, c);
}

显然，对于这道题，n=10

5.求解方程

求非线性方程\cos x -x =0在区间[0,1]内的根，误差不超过0.5 \times 10^{-6}

这道题要求求解非线性方程，我们的第一想法肯定是按照精度去遍历，不过显然这样的时间复杂度会很高，所以我们可以另辟蹊径，使用牛顿迭代法，牛顿迭代法只可以在单调函数上使用，我们不妨简单证明一下，记f(x)=\cos x-x （0 \leqslant x \leqslant 1）则 f'(x) = -\sin x -1，显然，在[0,1]内 f'(x)<0，所以f(x) 在[0,1]上单调递减，所以我们可以使用牛顿迭代法求解该方程的解。我们给定一个初始的近似解 x=0，根据牛顿迭代法有x_n=x_{n-1}-\frac{f(x_{n-1})}{f'(x_{n-1})}，我们只需要输出满足|f(x_n)-0|\leqslant0.5\times10^{-6}相应的x_n即可，我们定义一个计算x_n的函数，不断使用这个函数更新x即可。另外通过简单的证明可以得出这个函数在实数域上有且仅有一个零点，所以不必对x的范围做出判断。

#include <stdio.h>
#include <math.h>
#define EPSILON 0.5e-6

double solve(double x){
    double ret;
    ret = x-((cos(x)-x)/(-sin(x)-1));
    return ret;
}
int main(){
    double x = 0;
    while(!(fabs(cos(x)-x-0)<EPSILON)){
        x = solve(x);
    }
    printf("%.6lf\n", x);
}

运行该程序的输出结果为

0.739085

使用desmos得出的解

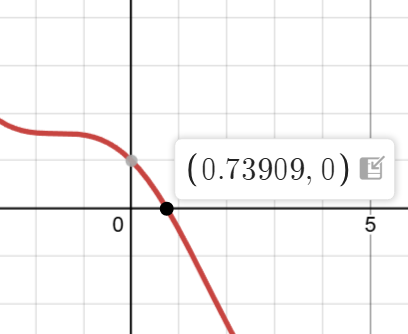
可通过修改EPSILON常量的值来得到更高的精度，事实上，除了使用牛顿迭代法以外，二分法也是一种不错的选择

6.数字三角形

编程打印如下数字图案：

                1 
              1 2 1
            1 2 3 2 1
          1 2 3 4 3 2 1
        1 2 3 4 5 4 3 2 1

我们不妨解决该数字三角形有N层的情况，我们观察这个图案每一行(记为i)的构造：

1.2\times(N-i)个空格。

2.从1到i的正序自然数，每个数用空格分隔。

3.从i-1到1的倒序自然数，每个数用空格分隔。

4.换行符。

在分析完后，我们就可以很轻松的实现代码

#include <stdio.h>

int main(){
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= 2*(n - i); j++){
            printf(" ");
        }//打印空格
        for (int k = 1; k <= i;k++){
            printf("%d ", k);
        }//打印正序数字
        for (int l = i - 1; l >= 1; l--){
            printf("%d ", l);
        }//打印倒序数字
        printf("\n");
    }

}

输入N为9时的输出(当N大于等于10时，由于出现了两位数，所以图案会有变形)

                1 
              1 2 1
            1 2 3 2 1
          1 2 3 4 3 2 1
        1 2 3 4 5 4 3 2 1
      1 2 3 4 5 6 5 4 3 2 1
    1 2 3 4 5 6 7 6 5 4 3 2 1
  1 2 3 4 5 6 7 8 7 6 5 4 3 2 1
1 2 3 4 5 6 7 8 9 8 7 6 5 4 3 2 1

7.九九乘法表

打印如下九九乘法表

    1      2      3      4      5      6      7      8      9      
----------------------------------------------------------------------------------------------------------------------
1 | 1x1=1  
2 | 2x1=2  2x2=4  
3 | 3x1=3  3x2=6  3x3=9  
4 | 4x1=4  4x2=8  4x3=12 4x4=16 
5 | 5x1=5  5x2=10 5x3=15 5x4=20 5x5=25 
6 | 6x1=6  6x2=12 6x3=18 6x4=24 6x5=30 6x6=36 
7 | 7x1=7  7x2=14 7x3=21 7x4=28 7x5=35 7x6=42 7x7=49 
8 | 8x1=8  8x2=16 8x3=24 8x4=32 8x5=40 8x6=48 8x7=56 8x8=64 
9 | 9x1=9  9x2=18 9x3=27 9x4=36 9x5=45 9x6=54 9x7=63 9x8=72 9x9=81

显然出题人的目的不是让我们直接将这个作为一个字符串打印出来，而是考察循环的相关知识，我们同样观察这个图案：

1.第1行为1~9，每个数中间6个空格

2.第2行为分割线，直接打印即可

3.第3~11行，我们不妨记为i行，在第i行，首先输出行标i，接上一个分隔符“|”，随后按顺序输出i\times k 及其的值，其中1\leqslant k \leqslant i 且为正整数，每个式子之间以空格隔开，每行最后接一个换行符（值得注意的是，为了保证对齐，如果乘积为个位数，我们需要打印两个空格）

#include <stdio.h>

int main(){
    printf("    ");
    for (int i = 1; i <= 9; i++){
        printf("%d", i);
        printf("      ");
    }
    printf("\n----------------------------------------------------------------------------------------------------------------------\n");
    for (int i = 1; i <= 9; i++){
        printf("%d | ", i);
        for (int j = 1; j <= i; j++){
            printf("%dx%d=%d",i,j,i*j);
            if((i*j)<10){
                printf("  ");
            }else{
                printf(" ");
            }
        }
        printf("\n");
    }
}

8.计算\pi的近似值

利用下列公式计算并输出\pi的值，取 n=10000
\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots + \frac{1}{4n - 3} - \frac{1}{4n - 1}

我们不妨记S_n = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots + \frac{1}{4n - 3} - \frac{1}{4n - 1}，于是这个可以看作数列a_n=\frac{1}{4n - 3} - \frac{1}{4n - 1}，前n项和，所以我们直接用循环累加即可

#include <stdio.h>

double sum(int n){
    double result = 0.0;
    for (int i = 1; i <= n; i++){
        result += 1.0/(4.0*i-3.0)-1.0/(4.0*i-1.0);
    }
    return result;
}
int main() {
    int n;
    scanf("%d", &n);
    double PI;
    PI = 4 * sum(n);
    printf("%.6lf\n", PI);
}

除此之外，我们也可以用递归的方法求解，由数列的性质有S_n=S_{n-1}+\frac{1}{4n - 3} - \frac{1}{4n - 1}，基于这个递推公式，我们可以用递归算法

#include <stdio.h>

double sum(int n){
    if (n == 1){
        return 2.0 / 3.0;
    } else {
        return 1.0/(4.0*n-3.0)-1.0/(4.0*n-1.0)+sum(n-1);
    }

}
int main() {
    int n;
    scanf("%d", &n);
    double PI;
    PI = 4 * sum(n);
    printf("%.6lf\n", PI);
}

不过值得注意的是，当n过大时，递归算法会栈溢出（实测大约在31000左右）

9.计算\sin x

计算正弦函数sin(x)的值，其中x从键盘输入。按下述公式计算，直到最后一项的绝对值小于1e-7时为止。
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots

其实这个题目与上面那个基本思路一样，同样可以看作数列a_n=\frac{x^{2n-1}(-1)^{n+1}}{(2n-1)!}的前n项和，按照第八题的思路求解即可，另外这道题还需要实现一个阶乘函数，可以用递归也可以用迭代

#include <stdio.h>
#include <math.h>
#define EPSILON 1e-7

int factorial(int n){
    int ret = 1;
    for (int i = 1; i <= n; i++){
        ret *= i;
    }
    return ret;
}//阶乘函数

double my_sin(double x){
    double fin=1.0;
    double ret=0.0;
    int n=1;
    while (!(fabs(fin-0)<EPSILON)){
        ret += pow(x,2*n-1)*pow(-1,n-1)/factorial(2*n-1);
        fin = pow(x,2*n-1)*pow(-1,n-1)/factorial(2*n-1);
        n++;
    }
    return ret;
}

int main(){
    double x;
    scanf("%lf", &x);
    printf("%.9lf\n", my_sin(x));
}

顺便吐槽一下，题目给的精度也太高了吧！！！！x取大一点就会溢出（甚至取不到1.5），建议读者可以取低一点的精度，或者把阶乘函数的返回值改为long long

10.回文数

编程输出100~10000之间的整数m ，满足m 、m \times m和m \times m \times m都是回文数

这个题目的难点在于如何判断回文数，如果我们要判断回文数，我们就需要将输入的整数倒序输出，然后判断其是否与原来的数相等，我们应该怎么对整数取反呢？不妨这样思考，我们可以先将数m取除以10的余数，这样我们就可以得到它的个位数字，然后我们再对它整除以10，就可把最后一位去掉，这样循环往复，我们就可以得到每一位数，然后我们可以通过乘以10将其放在正确的位数上。

#include <stdio.h>

int reverse(int n){
    int ret=0;
    while (n!=0){
        ret = ret * 10 + n % 10;//将得到的个位数加上并进位
        n /= 10;//削减位数
    }
    return ret;
}

int main(){
    for (int i = 100; i <= 1000;i++){
        if (i==reverse(i)&&i*i==reverse(i*i)&&i*i*i==reverse(i*i*i)){
            printf("%d\n", i);
        }
    }
}